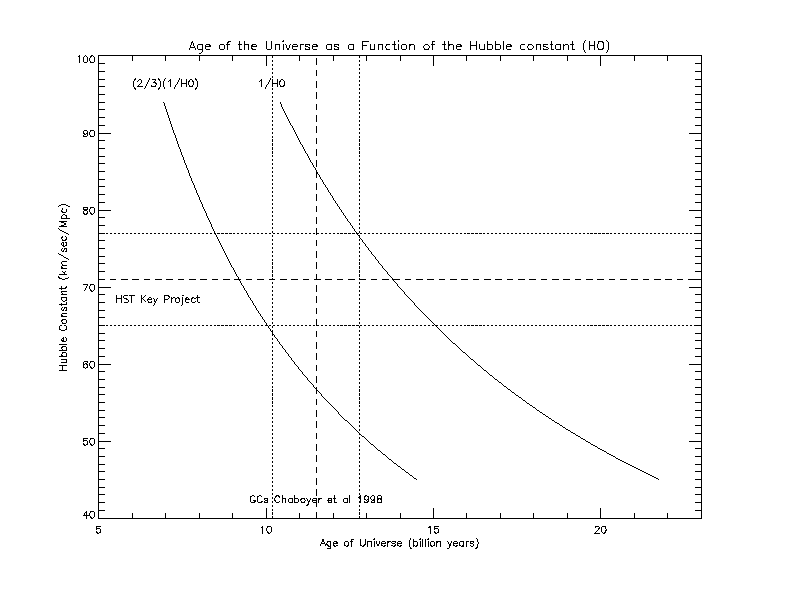
Fig 1: The Age of the Universe as a Function of the Hubble Constant
| Introduction |
Theories in modern cosmology center around the primary interpretation of cosmological redshift as an indication that the universe is expanding. If it is expanding outward, then it stands to reason that it must have started expanding at some point (just run your imaginary clock backwards), and leads to the notion now widely known as the big bang, the idea that all of the universe we know was born from a unique event at some time in the past. Classical general relativity is singular at that event (which means that the natal event cannot be described either mathematically or physically within the bounds of classical general relativity).
Current research is trying to combine the very successful ideas of quantum mechanics with the very successful ideas of general relativity. But just because these ideas are very successful independently does not mean that combining them is easy, and the effort is a long way from finished; for now we are stuck with an inscrutable big bang, followed by an expanding universe.
While the natal event may be beyond our reach, the universe becomes accessible to our understanding immediately thereafter. We can reach back through time as close as one Planck time (5.3906×10-44 seconds) after the bang. That being the case, there should be a purely cosmological way to figure out how old the universe is, or how long it has been since that inscrutable natal event.
| Introduction to H0 |
The Hubble constant (H0) is a measure of the expansion rate of the universe, commonly given in units of kilometers per second per megaparsec (km/sec/Mpc or km s-1 Mpc-1). Km/sec is a unit of velocity, and Mpc is a unit of distance (one parsec = 3.26 light years, so 1 Mpc = 3.26 million light years, and 1 light year is 9.4606x1015 meters or 5.8787x1012 miles). So H0 measures the expansion velocity of the universe (km/sec) as a function of the distance (Mpc) from the observer. Suppose that the value of H0 is 70 km/sec/Mpc. At a distance of one Mpc, we should see an expansion velocity of 70 km/sec (and the concordant spectral redshift). At two Mpc we should see a velocity of 140 km/sec. At 3½ Mpc we should see a velocity of 245 km/sec, and so forth. The larger the distance, the greater the expansion velocity.
Galaxies & galaxy clusters are subject to two kinds of motion, the cosmological expansion (commonly called the Hubble Flow), and local turbulent motions induced by the gravitational attraction of surrounding matter. Since the age of the universe is tied to its rate of expansion, we need to be able to separate those two components of motion, and consider only the Hubble flow. Since the cosmological expansion velocity increases with distance, then it stands to reason that we want to look out as far as we can.
| Cosmology and the Age of the Universe |
If the universe had no mass in it at all, and was therefore totally open, the age of the expanding universe would be expressed as follows, in terms of the Hubble Constant (H0):
where "age" is the age of the universe in years, and H0 is the Hubble constant in the usual units of km/sec/Mpc. The scale factor 1.023 x 10-12 is the product of 3.242 x 10-20 (Mpc/km) times 3.154 x 10+7 (sec/year), which is the unit conversion needed to make the age come out in years.
But of course, we know that the universe is not massless and therefore fully open because we are in the universe, and we have mass, and so do the stars and galaxies that we see. So that equation really represents a limit to the age of the universe. For a given value of H0 we know that, at least according to standard theory, the universe cannot be older than the value obtained by that equation.
If the average mass density of the universe is exactly equal to the critical density, then the universe is on average geometrically flat, and will expand forever. But it will slow its expansion asymptotically, because of the constant pull of gravity between the galaxies as they expand, stopping after an infinite time. So in practice, under such conditions, the universe will expand forever, slowing all the while. If that is the case, then the age of the universe is just 2/3 of the age from the equation given above. Observation indicates that in fact, the average mass density of the universe is about 20% of the critical density, quite a bit short of the mass density required to get the universe from its massless 1/H0 age to the critical mass age of 2/3 x 1/H0 (that 20% includes all of the dark matter that we can detect through its gravitational interactions).
And so we are led to the conclusion that the true age of the universe lies somewhere between 1/H0 and 2/3 x 1/H0. But H0 is a measurable quantity, so if we can make some observations that tell us what H0 is, then we can derive from that an age of the universe. Note that this age is derived from purely cosmological considerations and does not involve any reckoning of what stars & galaxies are made of, or how they are constructed, beyond the fact that they exert gravitational forces on each other.
| The First HST Value of H0 |
Flashback to 1994 when this paper hit the stands:
Distance to the Virgo Cluster Galaxy M100 from Hubble Space Telescope Observations of Cepheids
by W.L. Freedman et al.Nature 371(6500): pp757-762 (1994 October 27)
Abstract
Accurate distances to galaxies are critical for determining the present expansion rate of the Universe or Hubble constant (H0). An important step in resolving the current uncertainty in H0 is the measurement of the distance to the Virgo cluster of galaxies. New observations using the Hubble Space Telescope yield a distance of 17.1±1.8 Mpc to the Virgo cluster galaxy M100. This distance leads to a value of H0 = 80±17 km s-1 Mpc-1. A comparable value of H0 is also derived from the Coma cluster using independent estimates of its distance ratio relative to the Virgo cluster.
This was the first paper published by the Hubble Space Telescope Key Project on the Extragalactic Distance Scale; an ambitious effort to determine the value of the Hubble Constant to within an uncertainty of ±10%, this project was one of the driving forces behind the desire to put the Hubble Space Telescope in orbit in the first place. Coming at a time when just about everybody was happy with a value for H0 around 65 km/sec/Mpc, 80 was a real eye-opener. If you go back to the equation and look at what it means for the age of the universe, it means somewhere between 10 billion and 15.5 billion for a massless universe (the oldest allowed age range), or between 6.5 billion and 10 billion for a critical mass universe (the youngest allowed age range). But astronomers at the time thought that the oldest globular clusters we typically 15 billion years old, at the end of the age range scratched by this report only for a massless universe. Hence the appearance of an uncomfortable conflict: the oldest stars that we could see in the universe seemed to be older even than the universe itself, hardly a sound scientific idea. Something had to give.
| How Do We Know the Age of a Star? |
Figuring out the age of your favorite star is not so straightforward in concept as figuring out the age of the universe. While measuring H0 is quite difficult, once you have it, the age of the universe comes out in one little equation. But not so for stars.
The age of a star is derived through the process of stellar evolution. If we create a mathematical & physical model of the structure of a star, we quickly discover that stars are not static objects. Indeed, they can't be static objects. Stars derive their energy by nuclear fusion (a process we copied to make hydrogen bombs). The fusion, for instance, of hydrogen nuclei (single protons) into heavier helium nuclei (2 protons & 2 neutrons) releases more energy than it takes to get them to fuse in the first place (an exothermic reaction). So if you have a great deal of hydorgen laying around, and enough energy to get it all to fuse into helium, you can get back out a lot more energy than you put in. This process of gaining energy via nuclear fusion becomes less and less efficient as the nuclei get heavier, until you reach iron. Once you get to iron, it doesn't work anymore; after iron it takes more energy to make nuclei fuse than you will get in return (so the reaction is called endothermic). The total amount of nuclear fuel available decreases as the star uses it up, and so does the distribution of available fuel spread out inside the star. As those change, the internal temperature, pressure, and other physical characteristics of the star change radically. This also changes the visible characteristics at the surface of a star. So, in general, one can look at a star and see where it is in the course of its evolution. Note that here, the word evolution refers to the changes over time of a single star in its own lifetime, and not to the characteristics of a population over many generations, as the word is used in biological evolution (where it is said that "individuals do not evolve, populations do").
By the appropriate application of physics it is possible to follow the changes in a star's internal structure & chemistry, as well as its outward appearance, as it ages through its own lifetime. But all of the details need to be attended to, this is one area where it's hard to get away with simplifying approximations. Everything counts, and as a result the computational effort is extraordinary. The advent of faster and more powerful supercomputers has had a major effect on the study of stellar evolution.
The easiest things to measure about a star are color, and brightness as a function of color. The color and temperature are strongly related, so knowing the color gives the temperature. It turns out that if you measure the color and brightness of all the stars you can, and then just plot them all, the result is extremely non-random. Stars do not have just any old color and brightness. The two are distributed together in a representation we call the Hertzsprung-Russell diagram, or HR diagram for short.
The HR diagram is purely observational. Computational stellar evolution is the application of a great deal of fundamental physics to track the myriad of internal properties of a star as it ages through its own lifetime. The great success story of computational stellar evolution is that it recreates the observational HR diagram in exquisite detail, even reproducing what appear to be minor details in the HR diagram. It is one of the great success stories of modern science. One of the side effects is that we can compare stars as we see them to stars as we compute them, and thereby derive the age of a star from its location on an HR diagram.
That's an outline of how we know what the age of a star is. But note that this age ignores the cosmological problems of redshift, and is derived purely through fundamental physics. But on the observational side, you need to know the true brightness, not just the apparent brightness, and to do that you need to know the true distance to a star to convert from apparent (observed) brightness to true brightness, which you would know if you were right next to the star; distance makes it look dimmer.
There has been a great deal of progress in recent years in understanding stellar evolution, and in particular the evolution of globular cluster stars, which are amongst the oldest stars that we know of. They are very far away, and so the distance is harder to measure and true brightness harder to derive. The European Space Agency's Hipparcos Mission has used trigonometric parallax measurements on an unprecendented scale to measure the distances to over 1,000,000 "nearby" stars, and thereby calibrate the bottom steps of the distance scale. One of the results was to reset the distance scale for globular culsters, and thereby the true brightnesses, and thereby the cluster ages. These results were finally reported in 1998.
The Age of globular clusters in light of Hipparcos - Resolving the age problem
by B. Chaboyer, P. Demarque, P.J Kernan & L.M KraussAstrophysical Journal 494(1)Part 1: pp96-110 (1998 February 10)
We review five independent techniques that are used to set the distance scale to globular clusters, including subdwarf main-sequence fitting utilizing the recent Hipparcos parallax catalog. These data together all indicate that globular clusters are farther away than previously believed, implying a reduction in age estimates. We now adopt a best-fit value M-epsilon (RR Lyrae stars) = 0.39±0.08 (statistical) at [Fe/H] = - 1.9 with an additional uniform systematic uncertainty of (+ 0.13)(- 0.18). This new distance scale estimate is combined with a detailed numerical Monte Carlo study (previously reported by Chaboyer et al.) designed to assess the uncertainty associated with the theoretical age- turnoff luminosity relationship in order to estimate both the absolute age and uncertainty in age of the oldest globular clusters.
Our best estimate for the mean age of the oldest globular clusters is now 11.5±1.3 Gyr, with a one-sided 95 % confidence level lower limit of 9.5 Gyr. This represents a systematic shift of over 2 sigma compared to our earlier estimate, owing completely to the new distance scale - a shift which we emphasize results not only from the Hipparcos data. This now provides a lower limit on the age of the universe that is consistent with either an open universe or with a flat matter-dominated universe (the latter requiring H0 less than or equal to 67 km s-1 Mpc-1). Our new study also explicitly quantifies how remaining uncertainties in the distance scale and stellar evolution models translate into uncertainties in the derived globular cluster ages. Simple formulae are provided that can be used to update our age estimate as improved determinations for various quantities become available. Formulae are also provided that can be used to derive the age and its uncertainty for a globular cluster, given the absolute magnitude of the turnoff or the point on the subgiant branch 0.05 mag redder than the turnoff.
This is the most recent full study on the globular cluster age problem published to date. As you can see from the comments in the abstract, it's not just Hipparcos distances, but other effects have been updated as well, such as the effect of metallicity on brightness determinations (in the jargon of astronomers, anything heavier then helium is by definition a "metal"). This study puts the ages of the oldest globular clusters in the range 10.2 to 12.8 billion years. Since the 1994 HST Key Project age would range roughly from 10 to 15 billion years for an empty universe, and we are at about 20% of the critical density, it would already appear that the major conflict has been dealt with by advances in "ordinary" astrophysics.
However, that 1994 paper does not represent the end of the HST Key project effort. Rather, it was the first in a long series of papers describing their research efforts. In the summer of 1999 the HST key project announced that it had achieved its goal of determining the value of H0 with a 10% or better uncertainty.
| The HST Key Project and the Age of the Universe |
In order to fully understand the impact of the HST Key Project on our understanding of the age of the universe, we have to start with an all too brief description of the cosmic distance ladder. For objects that are relatively nearby, we can measure the distance directly using trigonometric parallax. For objects slightly farther away, we use cepheid class variable stars, which are known to exhibit a fixed relationship between true brightness and period of variability; we measure the period, and from that derive a brightness. By comparing the true brightness to the apparent brightness, we derive the distance. For objects still farther away, we derive distances from assumptions based on the more nearby objects. So the chain of assumptions gets longer the greater the distance gets. The result is that large distances become more uncertain, and the chain of reasoning gives rise to the cosmic distance ladder. The major impact of the Hipparcos mission was that it provided the first systematic parallax distances to a set of cepheid variable stars, thus tying together the two distance scales at last.
In particular, there are relatively few galaxies that are close enough for us to get the distance without reference to the redshift (so we can use those distances to calibrate the relationship between distance and redshift). Hubble solved the problem by using the 100 inch Hooker telescope at the Mt. Wilson Observatory (at that time the largest telescope in the world) to observe Cepheid class variable stars in a few nearby spiral galaxies, such as M31 & M33. A considerable improvement in observing techniques, imaging, and telescopes (the Keck I & II telescopes are 4 times the aperature and 16 times the collecting area of the 100 inch), has allowed modern astronomers to stretch the cepheid distance scale farther out than Hubble could. The larger the range of distance we have to compare with redshift, the better. But a problem still remained.
The problem is that the redshift measure the motion of the galaxy away from us, but that motion has two components. One of those components is the expanding universe carrying the galaxy along for the ride. The other component is local motion induced by the combined gravitational tug of the galaxies surrounding the observed galaxies. To determine the rate of expansion of the universe (expressed as H0) we want to compare distance to the component induced by the expanding universe, and we want to eliminate the local component. The local component becomes smaller at greater distances, so if we can measure larger cepheid distances, we can get a better sampling of the cosmological expansion, and a better calibration of the relation between cosmological expansion and distance. And that gives a better value for H0, and therefore the age of the universe.
The idea behind the HST Key Project was to use the unprecedented capability of the Hubble Space Telescope to observe and measure cepheid variable stars in distant galaxies, observations not possible from underneath the Earth's atmosphere. Five years, 18 galaxies, and nearly 30 published papers later, the HST Key Project announced in the summer of 1999 that it had met its goal. They reported H0 = 71±6 km/sec/Mpc. The result is not uncontroversial; the group led by Sandage & Tammann continues to hold out for a smaller value of H0 (more like 60 km/sec/Mpc), and consequently an older universe.
| Interim Conclusion: The Age of the Universe |

In the discussion on cosmology and the age of the universe, I gave the equation(s) for figuring out the age of the universe from cosmological theory, given a measurement of the Hubble Constant. Figure 1 above shows these two equations plotted on the field of age vs H0; a curve for 1/H0 and another for 2/3 of that. Remember that the true age of the universe lies along a curve that is somewhere between these two curves. The horizontal bar traces out the range of H0 as determined by the Key Project, 71±6 km/sec/Mpc. The two combine to form a region bounded on the right & left by the two theoretical curves, and on the top and bottom by the range of values for H0 as reported by the Key Project. If the Key Project results are correct, then the true age of the universe should lie on a curve roughly parallel to the ones on the right & left, passing through that region.
The vertical bar on figure 1 marks out the range of ages reported for the oldest globular clusters, as given by the Chaboyer et al. paper cited above. Although their result is derived entirely from the physics of stellar structure and evolution, with no input from cosmological theory, the vertical bar cuts right through the prime region selected by cosmologists as the place where the age of the universe should be found. It is a tour-de-force triumph for astrophysics & cosmology; two totally independent indicators for the age of the universe give concordant results.
But I labeled my conclusions as "interim" for good reasons. In 1994 globular cluster stars were generally accepted as the oldest stars we can see, but that is no longer the case. The last couple of years has seen an attempt to derive the ages of old metal-poor galactic halo stars (see for instance, "r-process abundances and chronometers in metal-poor stars" by J.J. Cowan et al., Astrophysical Journal 521(1): 194-205, Part 1, August 10 1999). The few reported ages are in the 15 billion year range; the cited paper by Cowan et al. gives 15.6±4.6 billion years, which covers the rather expansive range of 11.0 billion to 20.2 billion years. The range of ages allowed by the HST Key Project results falls just short of 15 billion, but the majority of the bottom half of the uncertainty range cited by Cowan et al. falls within the Key Project range. So even if we include the halo stars, there is still no major conflict between the cosmological and astrophysical ages for the universe. And if the accepted value of H0 should move downward (as Sandage & Tammann and others would have it), the older halo stars are even easier to accomodate. But the argument over H0 remains on the table.
| The Bottom Line |
The bottom line is that there is not now a conflict between the astrophysically determined ages of the oldest stars, and the cosmologically determined age of the universe. While there was one in 1994 it was predictably short lived. While it made good reading for the popular press, astronomers were already busy trying to find the right solution. The result was that the cosmological age moved up (as H0 moved down), through the addition of more and better data, and the astrophysical ages moved down, through the addition of more precise techniques and more detailed models. In short, we learned more about the problem, and exercised that knowledge to reach a new conclusion. But I think it is safe to say that the universe is definitely not less than 10 billion years old, and definitely not more than 20 billion years old, if the expanding universe and big bang cosmology is correct.
| Some Key Project Research Papers from 1999 |
| Some Sandage & Tammann Research Papers from 1999 |
| Web Sites of Interest |
Back to Tim Thompson's FAQ Page
Back to Tim Thompson's Home Page